Le equazioni di primo grado
Guida per il docente di sostegno e curricolare
presentazione didattica - educativa
Traguardi di competenza
• Risolvere problemi utilizzando equazioni di primo grado in contesti semplici.
• Comprendere il concetto di uguaglianza e di soluzione/i di un'equazione.
• Acquisire un metodo logico-sequenziale per risolvere problemi algebrici semplici.
Obiettivi disciplina
•Conoscenze: equazione, incognita, membri, tipi di soluzione (determinata, indeterminata, impossibile).
•Principi di equivalenza e applicazioni pratiche perrisolvere equazioni.
•Abilità: saper
tradurre semplici problemi dallinguaggionaturale in equazionidiprimogrado
Obiettivi dimensione
•Riconoscere i passaggi risolutivi in modo autonomo e pianificare strategie adeguate.
•Riflettere sul proprio metodo esulla capacità di orientarsi nella soluzione di
un problema
.
Obiettivi personalizzati / equipollenti
•Riconoscere un'equazione di primo grado e il concetto di soluzione/i.
•Saper applicare i principi di equivalenza per isolare l'incognita in equazioni numeriche intere semplici (x + a = b, ax = b, ax + b = c).
•Risolvere equazioni a coefficienti interi anche con l’incognita in entrambi i membri, senza utilizzare frazioni o parentesi complesse (utilizzare principi di equivalenza).
•Essere in grado di verificare la correttezza delle soluzioni.
•Libro di testo / schede semplificate «Le equazioni di primo grado» con indizi per il gioco «caccia al tesoro» da fornire alle studentesse/i.
•Bilancia algebrica (modello fisico), LIM, fogli, buste, oggetti concreti.
Panoramica delle attività
1) Introduzione (lezione frontale interattiva con esempi concreti)
2) Introduzione della «bilancia algebrica» per «visualizzare» i principi di equivalenza.
3) Esplorazione (laboratorio in piccoli gruppi) – «Caccia al tesoro delle equazioni»: a ciascun gruppo viene consegnata una prima busta contenente un’equazione da risolvere o un test o un compito di realtà – Le soluzioni corrette sono utilizzate per decodificare indizi che portano alla busta successiva. L’ultima busta porta a un «piccolo tesoro».
4) Formalizzazione (principi di equivalenza).
5) Applicazione e consolidamento (esercizi difficoltà progressiva).
6) Compito realtà (lavoro di gruppo).
7) Riconoscere le definizioni associate ai termini proposti.
8) Verifica, 9) Recupero, 10) Valutazione
Strategie di adattamento, facilitazione
e semplificazione
L’insegnante può fornire schede visive semplificate con esercizi parzialmente risolti, utilizzare i colori per distinguere i segni i coefficienti e le incognite; affiancare le studentesse e gli studenti in difficoltà; individuare compagne e compagni tutor durante il lavoro di gruppo.
Consentire l’uso della calcolatrice o di strumenti digitali compensativi e proporre esempi concreti e problemi reali legati agli interessi personali (crescita motivazione). Prevedere tempi distesi e privilegiare la spiegazione orale e visiva, rispetto alla sola produzione scritta.
Ulteriore sviluppo potenziale
L’insegnante può proporre un laboratorio interdisciplinare (con fisica, economia, tecnologia) su scenari reali che richiedano l’uso di equazioni per fare previsioni o stime; estendere l’attività a equazioni con frazioni, parentesi o con incognita in entrambi i membri; può utilizzare un ambiente di apprendimento digitale (ad esempio una escape room virtuale) per riprodurre la dinamica della caccia al tesoro in modalità online. Può chiedere infine di creare un quaderno delle regole e strategie risolutive condivisocontuttalaclasse.
Introduzione: esempi concreti
• Esempio: "Ho 7 caramelle, ne do alcune, ne restano 4." • Modello con equazione: 7 – x = 4 o x + 4 = 7 • Concetto: l'incognita è il valore sconosciuto (qui le caramelle date).
(uguaglianza) e principi di equivalenza
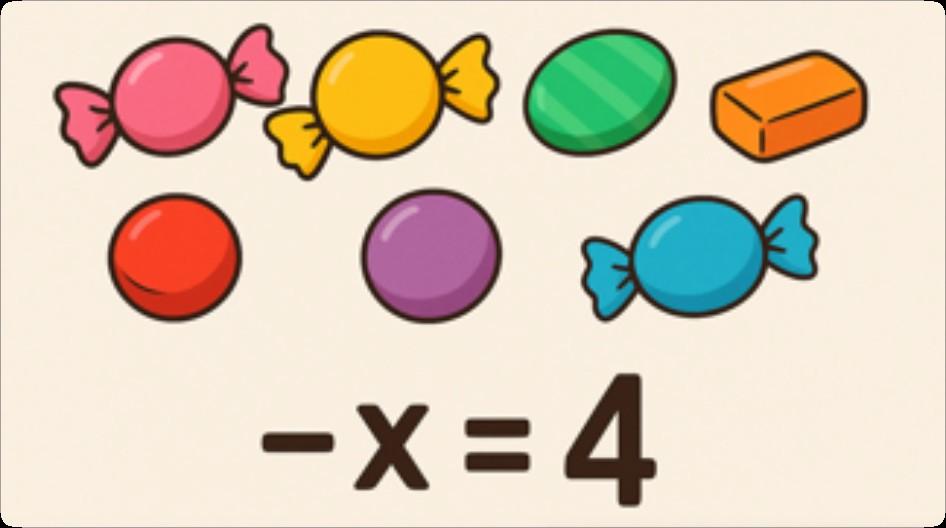
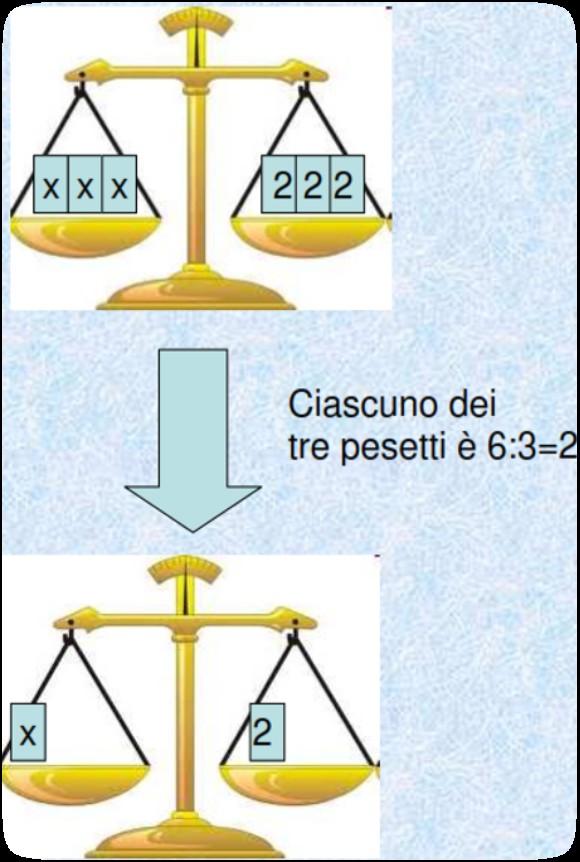
•La bilancia rappresenta l'uguaglianza: entrambi i piatti devono bilanciarsi.
•Aggiungere/sottrarre lo stesso peso su entrambi i piatti mantiene l'equilibrio (primo principio di equivalenza – regola del trasporto).
•Moltiplicare/dividere entrambi i membri per lo stesso numero (≠0) mantiene l'equilibrio (secondo principio di equivalenza).
Esempi di esercizi contenuti nelle buste (difficoltà crescente)
Inserisci accanto a ogni termine la lettera corrispondente alla sua definizione
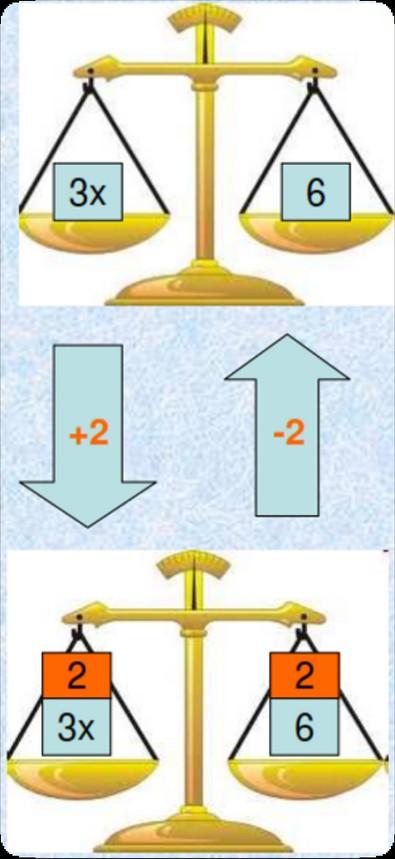
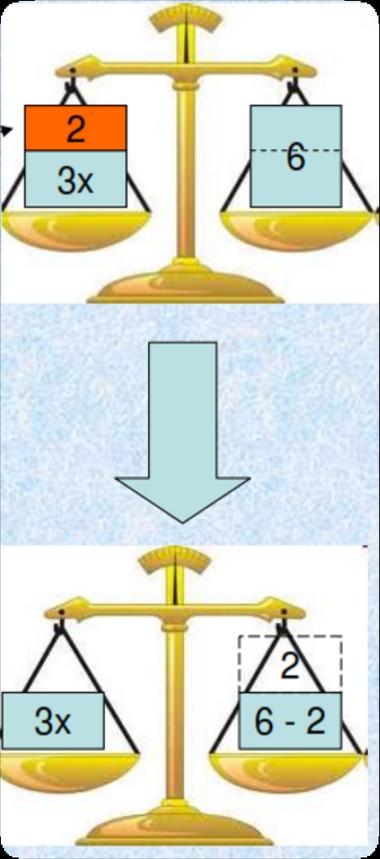
Compito di realtà
«Abbiamo comprato 3 pacchetti di figurine e ci sono avanzate 2 figurine. In totale avevamo 17 figurine. Quante figurine ci sono in ogni pacchetto?»
Impostare l’equazione sulla base dei dati del problema.
Recupero e facilitazioni
•Esercizisemplificaticonnumeripiùpiccoli emenopassaggi. •Uso di immagini, rappresentazioni concreteemappeconcettuali. •Tempi più lunghi, verifiche orali, tutoraggiotrapari.
Autovalutazione (esempio)
1. Ho partecipato attivamente alle attività del mio gruppo? (1-5; 1 MIN, 5 MAX)
2.Ho compreso come risolvere le equazioni di primo grado incontrate? (1-5)
3.Sono stato in grado di spiegare agli altri il procedimento risolutivo adottato? (1-5)
4.Ho trovato interessante l'attività? (1-5)
5.Ritengo di aver imparato qualcosa di nuovo? (15)
